DBBを用いた直角度誤差の測定
DBB測定とは
工作機械の精度検査を行う手法のひとつに、ボールバー(DBB)を用いた円運動精度試験があります。 DBBとは、両端に球(スタイラス)が付いたバーの伸縮によって機械の運動精度を測定する装置です。 DBBは2つの球と1本のバーで構成されており、 球の一方を主軸、他方をテーブルに取り付けた状態で、片方の球を中心として円弧補間運動をさせます。 2つの球の間の距離を連続測定することで、工作機械の運動精度を評価する仕組みです(ISO230-4)。
DBBで直角度誤差を測る
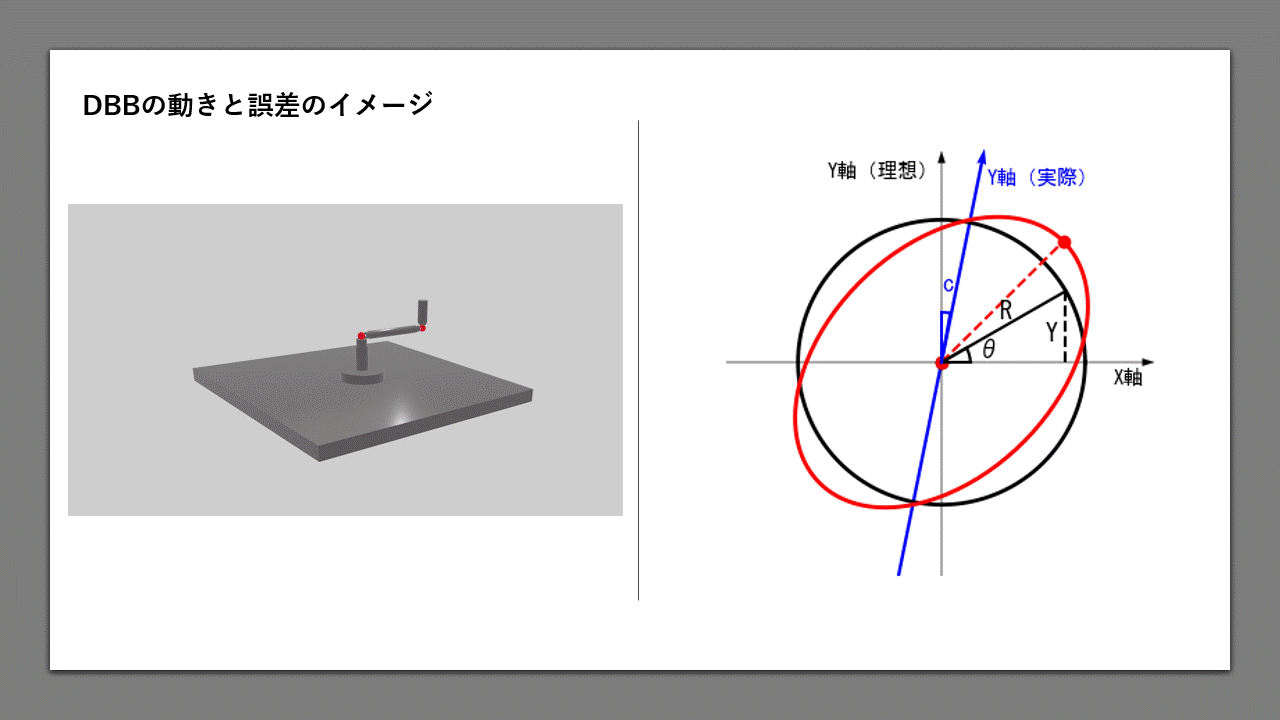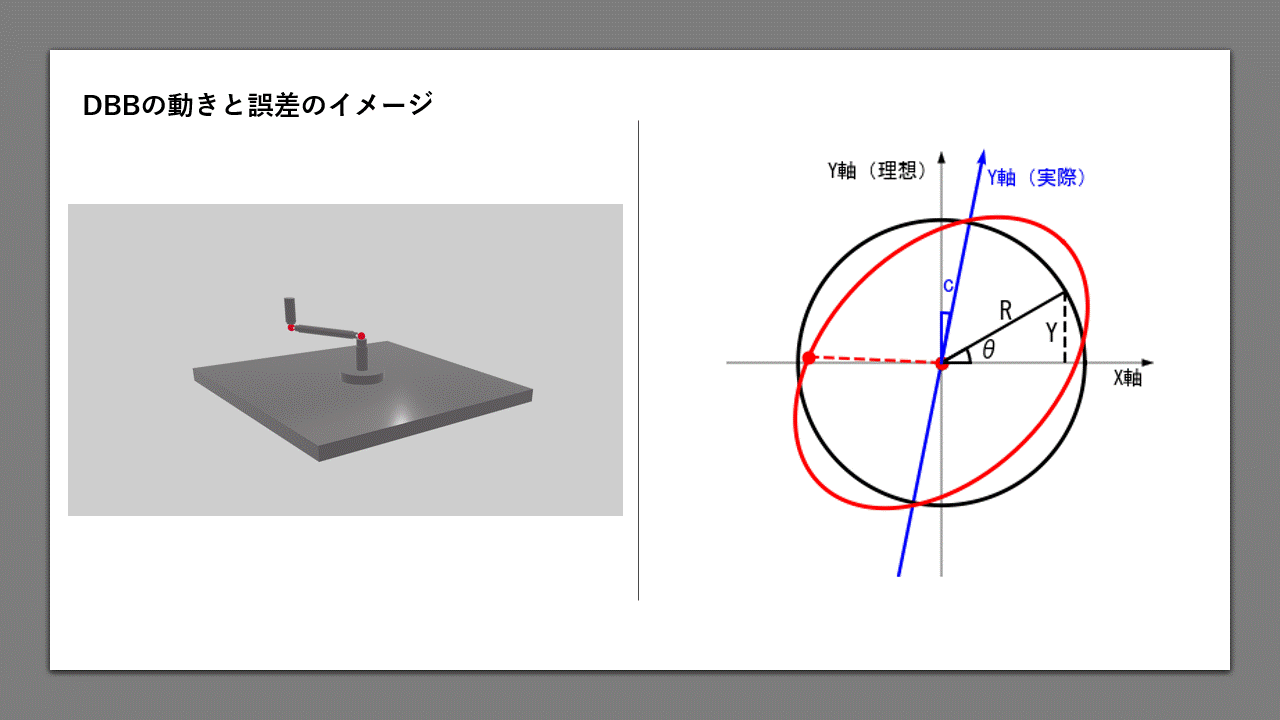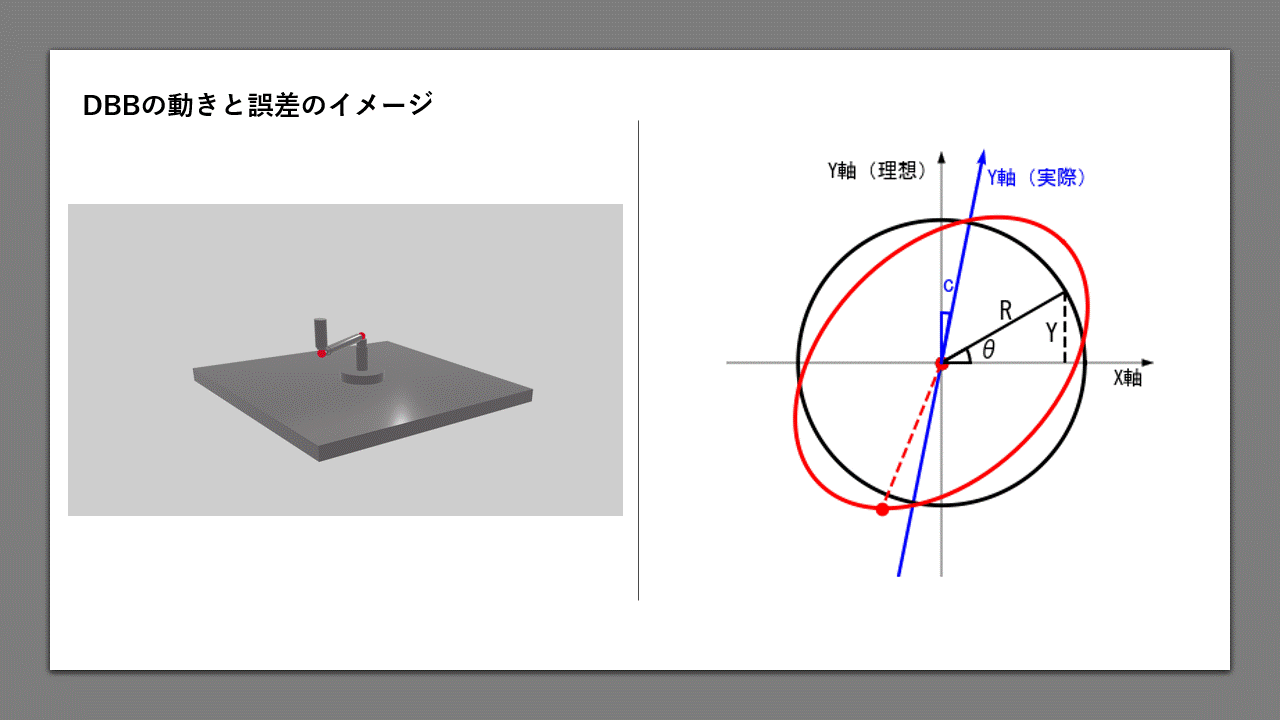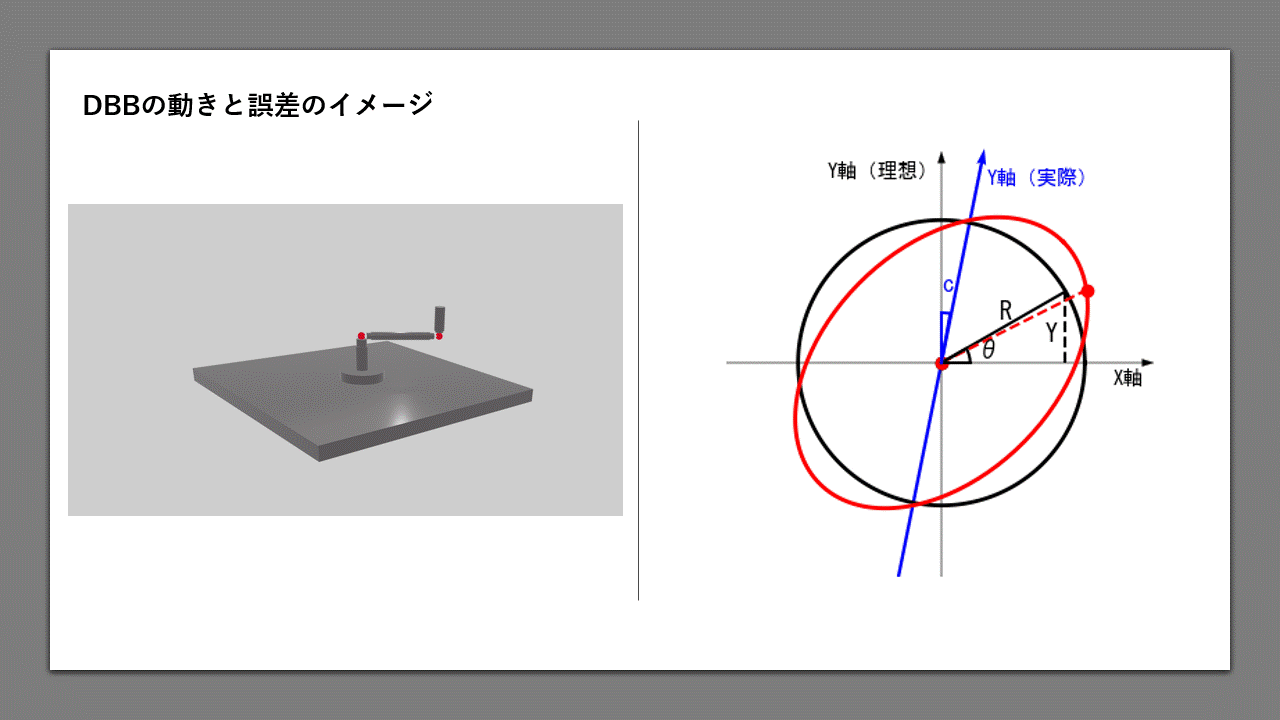
図1は、DBBの測定結果を模式的に表したグラフです。黒色のラインが理想値、赤色のラインが実測値で、
実際はさらに各位置での誤差が加わって、ギザギザした楕円状の形状になります。
このような測定結果のデータをもとに、単なる回転運動の精度だけでなく、直線運動誤差や平面誤差といった機械の運動精度を知ることができます。
ここでは例として、直角度誤差を取り上げます。
よく知られているように、この機械の直角度誤差は、45度方向の半径偏差(図の矢印部分) \(ΔR_{45}\) で表されます。
ではなぜ直角度誤差が45度方向に傾いて現れるのかをご存じでしょうか?
DBBの円運動の基準半径 \(R\) からの変化量 \(ΔR\) と、 各軸が有する運動誤差 \(ΔX\)、\(ΔY\) の関係は式(1)で与えられます。
\begin{equation} {(R+∆R)}^2 = {(X+∆X)}^2+{(Y+∆Y)}^2 \end{equation}
これを展開し、2次の微小項を省略すると、
\begin{equation} 2R∆R=2X∆X+2Y∆Y \nonumber \end{equation}
\begin{equation} ∆R=\frac{X∆X+Y∆Y}{R} \end{equation}
となります。 XY軸間の誤差要因として直角度誤差 \(c[μrad]\) のみを考える場合、\(c ≒ tanc\) として、 各軸の運動誤差は図2より次のようになります。
\begin{equation} ∆X=cY , ∆Y=0 \end{equation}
これらと \( X=R cosθ ,Y=R sinθ \) の関係を式(2)に代入すると、
\begin{equation} ∆R= \frac{cR}{2} \cdot \sin{2θ} \end{equation}
となります。
ここで\(∆R\)は \(\sin{2\theta}=1\)すなわち\(\theta= 45^{^\circ}\)で最大となります。
よって45度方向の半径方向偏差を\(∆R_{45}\)とすると、式(4)から直角度誤差は
\begin{equation} c= \frac{2∆R_{45}}{R} \end{equation}
で求めることができます。 つまり、直角度誤差がある場合、円運動の軌跡は45度方向に長軸を持つ楕円となり、 45度方向の長軸と基準円の半径の差から直角度誤差が求められることになります。