幾何誤差の成分表記 その1
空間精度の“幾何誤差”
マシニングセンタのNCプログラムへの指令値は 1μm単位で入力されます。しかし実際のところ、主軸に取り付けた工具先端の位置は、μmオーダーで見ると指令値通りではないことが残念ながらほとんどです。
ひとくちに機械の誤差と言っても、いくつかの要因があります。単軸上の位置が指令値とずれている(位置決め誤差)、まっすぐ軸を動かしているつもりでもふらついたりカーブしている(真直誤差)、スピンドルやテーブルの向きが場所によって違う(姿勢誤差)など、これらの誤差を総称して「幾何誤差」と呼びます。
工作機械は、程度の差こそあれ大なり小なり「幾何誤差」を持っており、複数の幾何誤差が重なり合って、加工誤差となってあらわれます。
今回は幾何誤差のうち、誤算運動の表記方法を確認してみましょう。(※軸平均線の幾何誤差については次回記事で取り上げる予定です。)
誤差の要素と表記
まずは誤差の表記ルールを次のように定めます。
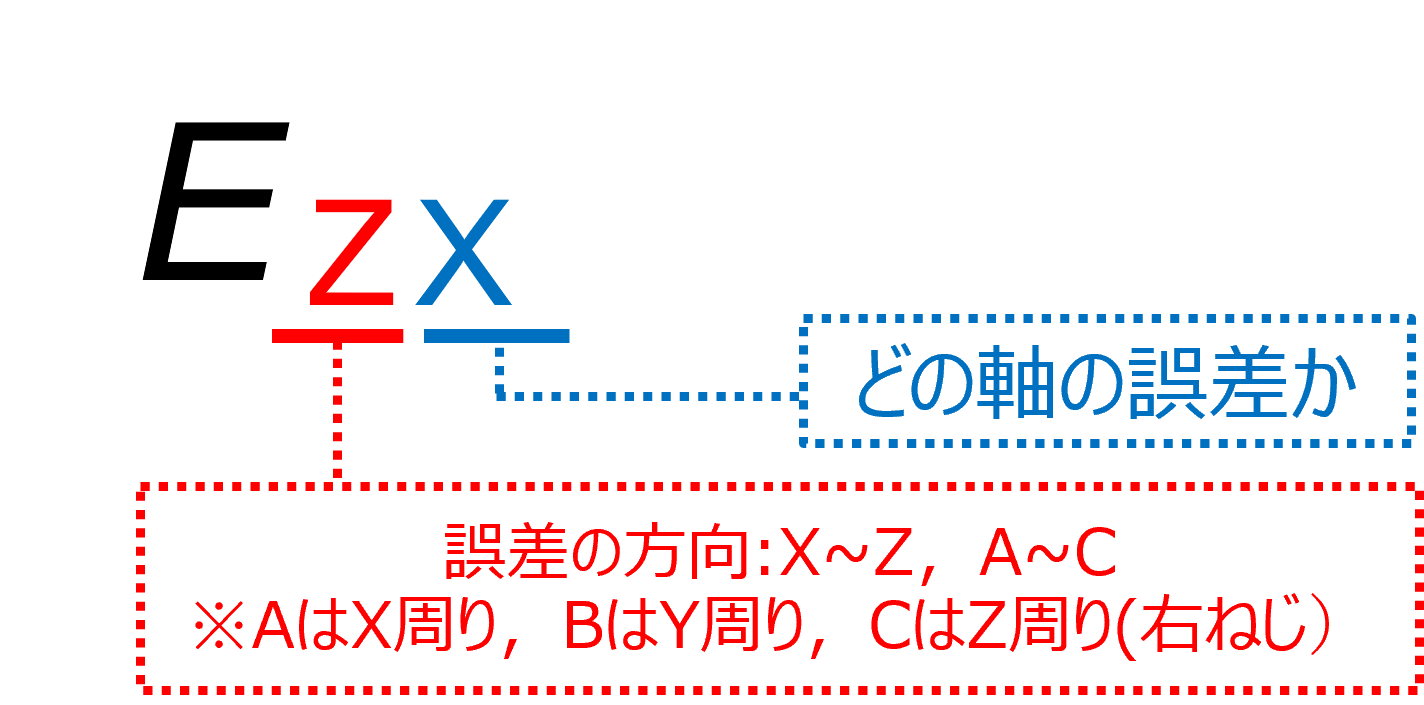
空間精度は、各軸の誤差成分の組み合わせで表現されます。どの軸まわりの誤差か(3軸)、どの方向の誤差か(3軸および3方向の回転)、それらをかけあわせることで計18種類の誤差表記となります。
例としてX軸まわりの6種類の誤差を見てみます。
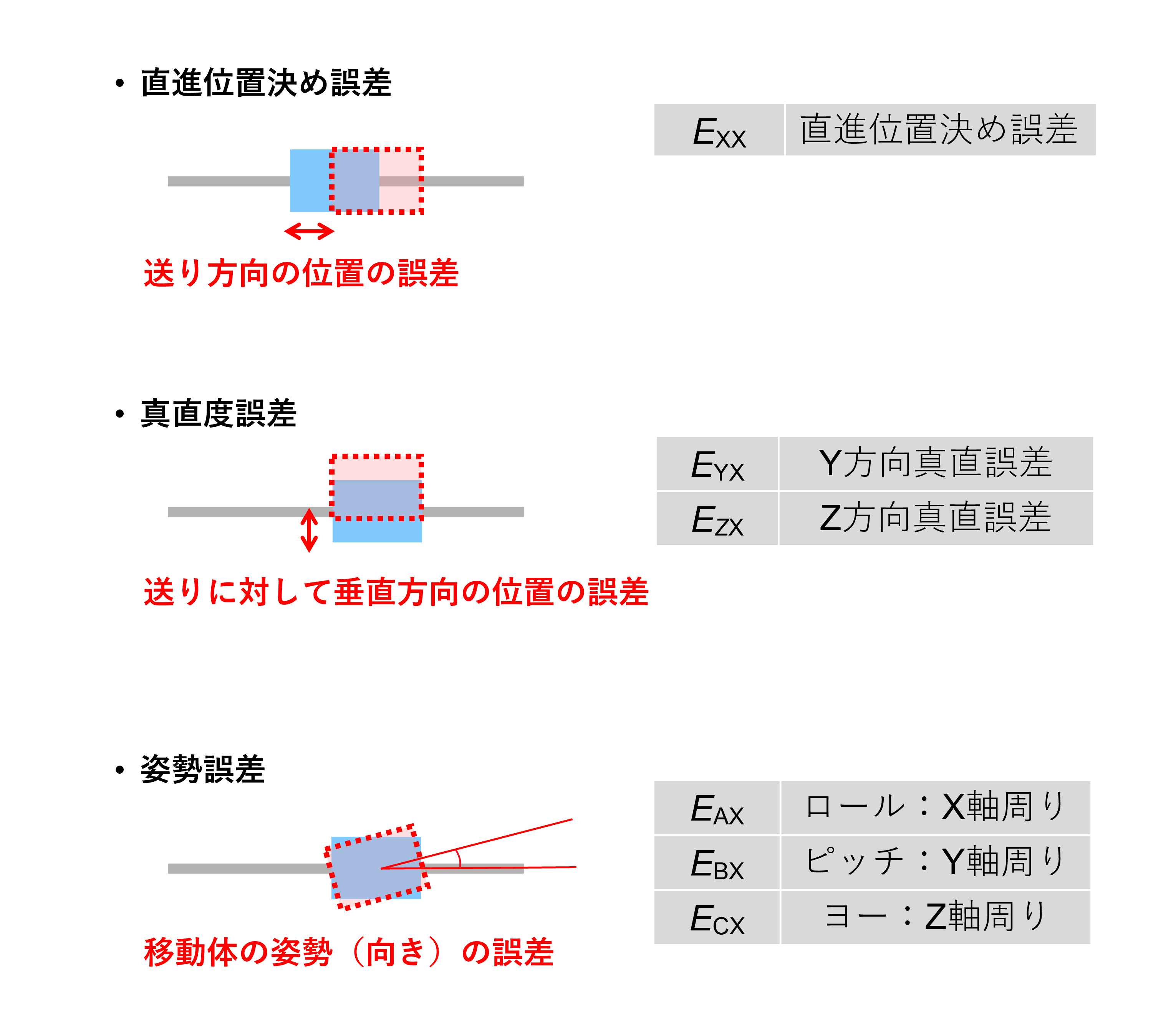
X軸まわりだけ取り出しても、上記6つの誤差が重なって実際の工具先端の誤差が生じることが分かります。これら6つの幾何誤差がX軸・Y軸・Z軸まわりに発生し、それぞれの誤差量は位置によって変化します。
上記のような単軸まわりの誤差に加え、2次元、3次元の空間では、各軸同士の誤差を考慮する必要があります。図のように、各軸に沿った動きの平均をとった直線(軸平均線)を考えます。2軸の軸平均線同士がなす角度は、当然理想的には直角です。軸平均線同士のなす角の、直角を基準とした誤差量が直角度誤差です。
誤差運動は軸に沿った運動に伴って変動しますが、直角度誤差は軸の移動によらず、その機械に固有の一定の値となります。
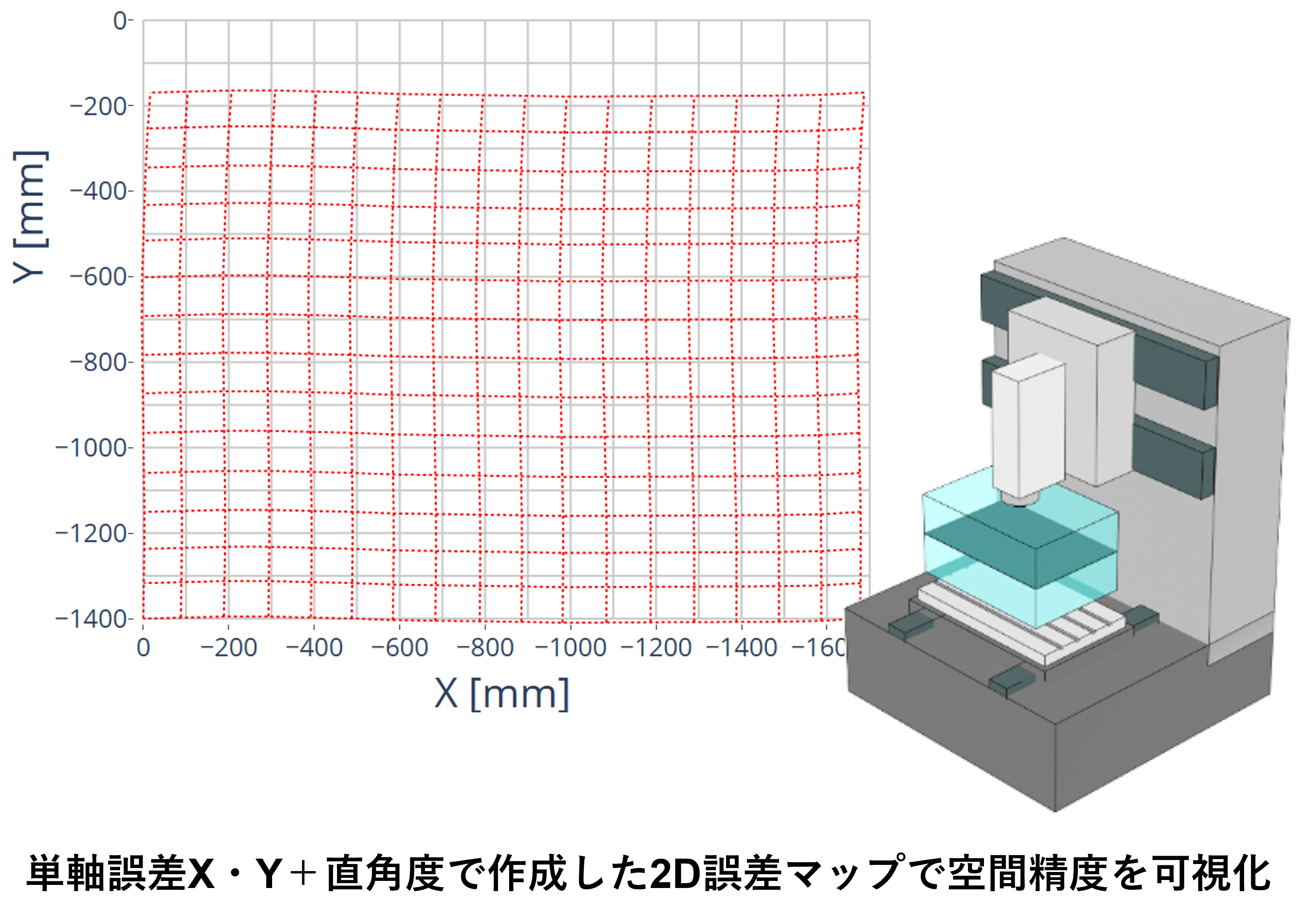
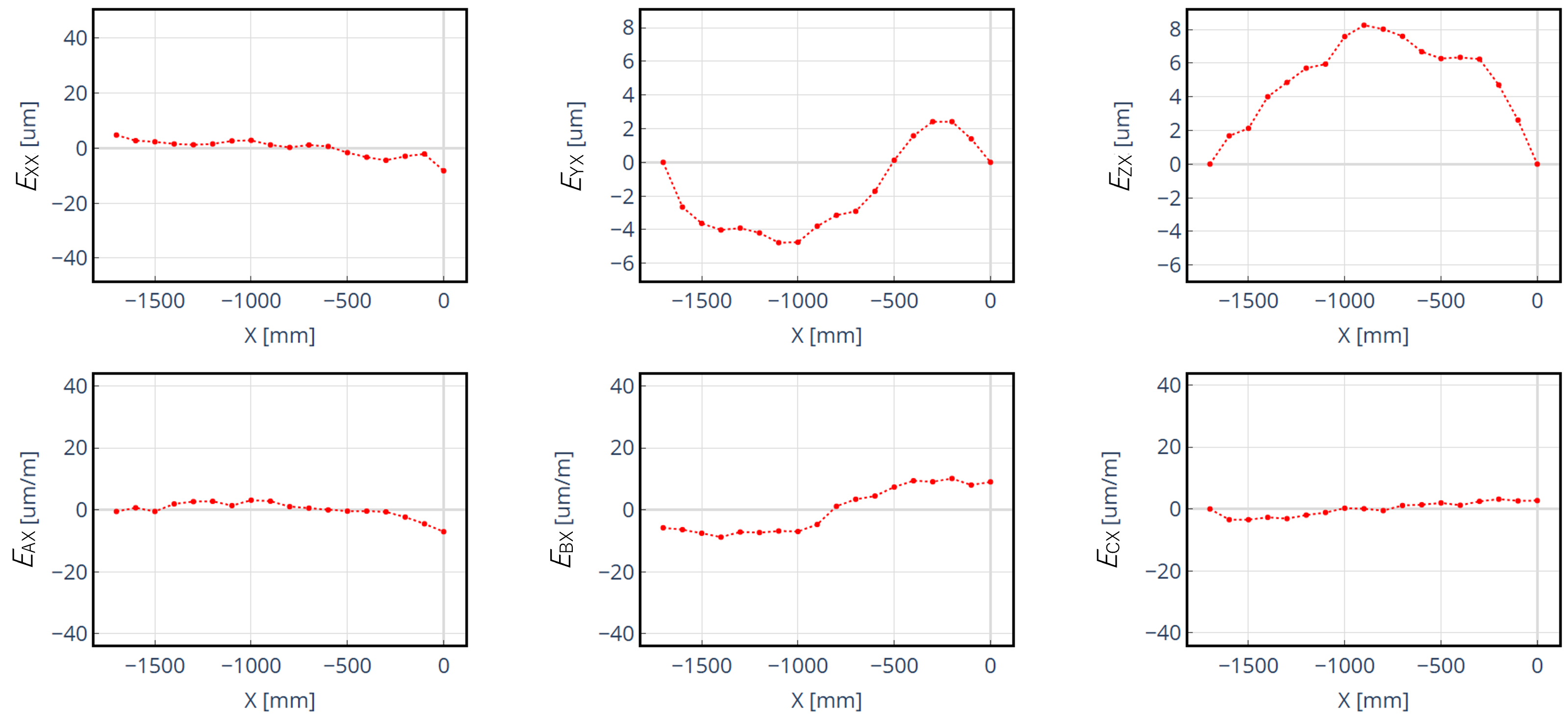
誤差の可視化
複雑な幾何誤差を把握するには、誤差量を可視化することが有効です。弊社の空間精度測定サービスでは、解析によって単軸誤差の要素をグラフ化します。
また、幾何誤差に直角度誤差を加えて2次元、3次元のイメージマップも作成できます。2次元誤差マップは任意の切り口で作成できるので、加工位置などに応じてどのような誤差分布になっているか確認することができます。